Here we report a half-quantized Hall effect in a metal or semimetal. The Hall conductance is half quantized and the longitudinal conductance is nonzero. Consequently, the Hall resistivity is not quantized. The half quantization occurs when the parity symmetry or time reversal symmetry emerges near the Fermi surface or Fermi level while the symmetry is broken in the whole system. A recent experiment reports the observation of the half-quantized Hall conductance in a magnetically-doped topological insulator. We discover that a single gapless Dirac cone exists in the band structure and has half-quantized conductance when the Fermi level intercepts the gapless surface states in which the parity symmetry is invariant. As there are no localized chiral edge states in the gapless and metallic system, we find that the chiral edge current is carried by the gapless surface states. The current density peaks at the edge and decays in a power law rather than the exponential decay as in the conventional quantum anomalous Hall effect. The half quantized Hall conductance is a signature of parity anomaly in a single gapless Dirac cone on a lattice. We term the nontrivial quantum phase as “parity anomalous semimetal”. The work opens the door to exploring novel topological states of matter with fractional topological invariants.


This work was supported by the National Key R&D Program of China under Grant No. 2019YFA0308603, the Research Grants Council, University Grants Committee, Hong Kong under Grant No. C7012-21G and No. 17301823; the and Quantum Science Center of Guangdong-Hong Kong Macau Greater Bay, China.
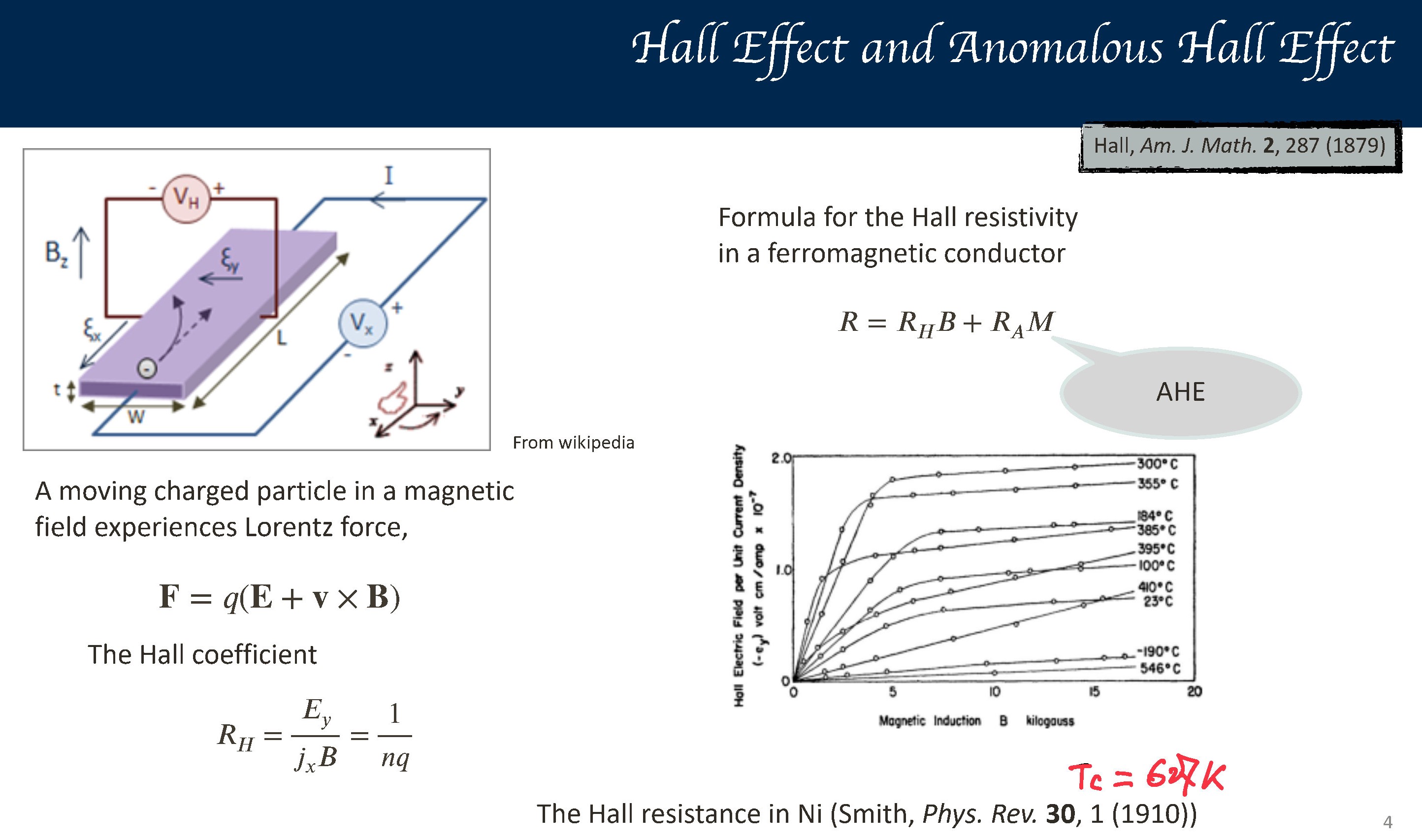
1. E.H. Hall, On a new action of the magnet on electric currents, Am. J. Math. 2, 287 (1879).
2. A.W. Smith, The variation of the Hall effect in metals with change of temperature, Phys. Rev. (Series I) 30, 1 (1910).
3. K.v. Klitzing, G. Dorda, and M. Pepper, New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance, Phys. Rev. Lett. 45, 494 (1980).
4. D.C. Tsui, H.L. Stormer, and A.C. Gossard, Two-dimensional magnetotransport in the extreme quantum limit, Phys. Rev. Lett. 48, 1559 (1982).
5. F.D.M. Haldane, Model for a quantum Hall effect without Landau levels: condensed-matter realization of the "parity anomaly", Phys. Rev. Lett. 61, 2015 (1988).
6. C.Z. Chang, J.S. Zhang, X. Feng, J. Shen, Z.C. Zhang, M.H. Guo, K. Li, Y.B. Ou, P. Wei, L.L. Wang, Z.Q. Ji, Y. Feng, S.H. Ji, X. Chen, J.F. Jia, X. Dai, Z. Fang, S.C. Zhang, J. He, Y.Y. Wang, L. Lu, X.C. Ma, and Q.K. Xue, Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator, Science 340, 167 (2013).
7. X.L. Qi and S.C. Zhang, Topological insulators and superconductors, Rev. Mod. Phys. 83, 1057 (2011).
8. A.N. Redlich, Parity violation and gauge noninvariance of the effective gauge field action in three dimensions, Phys. Rev. D 29, 2366 (1984).
9. G.W. Semenoff, Condensed-matter simulation of a three-dimensional anomaly, Phys. Rev. Lett. 53, 2449 (1984).
10. S.Q. Shen, Topological Insulators (Springer, 2012).
11. D.J. Thouless, M. Kohmoto, M.P. Nightingale, and M. den Nijs, Quantized Hall conductance in a two-dimensional periodic potential, Phys. Rev. Lett. 49, 405 (1982).
12. Q. Niu, D.J. Thouless, and Y.S. Wu, Quantized Hall conductance as a topological invariant, Phys. Rev. B 31, 3372 (1985).
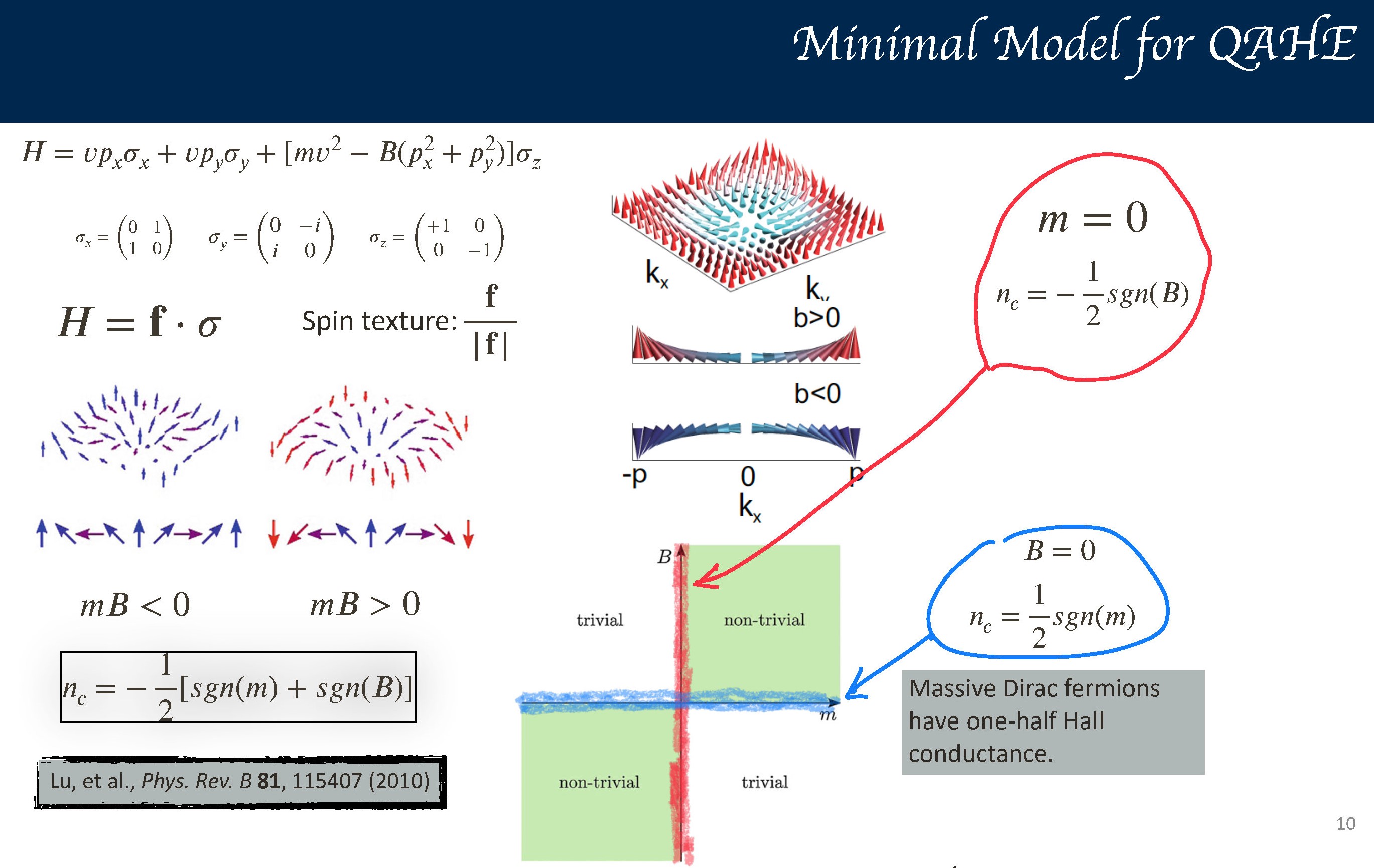
13. H.Z. Lu, W.Y. Shan, W. Yao, Q. Niu, and S.Q. Shen, Massive Dirac fermions and spin physics in an ultrathin film of topological insulator, Phys. Rev. B 81, 115407 (2010).
14. K.G. Wilson, Quarks: From paradox to myth. In: A. Zichichi, (eds) New phenomena in subnuclear physics. The Subnuclear Series, vol 13 (Springer, Boston, MA, 1977).
15. B. Fu, J.Y. Zou, Z.A. Hu, H.W. Wang, and S.Q. Shen, Quantum anomalous semimetals, npj Quantum Mater. 7, 94 (2022).
16. E. Fradkin, Field theories of condensed matter physics (Cambridge University Press, 2013).
17. J.Y. Zou, R. Chen, B. Fu, H.W. Wang, Z.A. Hu, and S.Q. Shen, Half-quantized Hall effect at the parity-invariant Fermi surface, Phys. Rev. B 107, 125153 (2023).
18. Y.L. Chen, J.H. Chu, J.G. Analytis, Z.K. Liu, K. Igarashi, H.H. Kuo, X.L. Qi, S.K. Mo, R.G. Moore, D.H. Lu, M. Hashimoto, T. Sasagawa, S.C. Zhang, I.R. Fisher, Z. Hussain, and Z.X. Shen, Massive Dirac fermion on the surface of a magnetically doped topological insulator, Science 329, 659 (2010).
19. M. Mogi, Y. Okamura, M. Kawamura, R. Yoshimi, K. Yasuda, A. Tsukazaki, K.S. Takahashi, T. Morimoto, N. Nagaosa, M. Kawasaki, Y. Takahashi, and Y. Tokura, Experimental signature of the parity anomaly in a semi-magnetic topological insulator, Nat. Phys. 18, 390 (2022).
20. H. Wang, B. Fu, and S.Q. Shen, Recent progress of transport theory in Dirac quantum materials, Acta. Phys. Sin. 72(17), 177303 (2023).
21. R. Chen and S.Q. Shen, On the half-quantized Hall conductance of massive surface electrons in magnetic topological insulator films, Sci. China - Phys. Mech. Astron. (2024).
22. E. Prodan, Disordered topological insulators: a non-commutative geometry perspective, J. Phys. A Math. Theor. 44, 113001 (2011).
23. J. Li, R.L. Chu, J.K. Jain, and S.Q. Shen, Topological Anderson insulator, Phys. Rev. Lett. 102, 136806 (2009).
24. J.Y. Zou, B. Fu, H.W. Wang, Z.A. Hu, and S.Q. Shen, Half-quantized Hall effect and power law decay of edge-current distribution, Phys. Rev. B 105, L201106 (2022).
25. B. Fu, K.Z. Bai, and S.Q. Shen, Half quantum mirror Hall effect, arXiv: 2402.02654 (2024).
26. K.Z. Bai, B. Fu, Z.Y. Zhang, and S.Q Shen, Metallic quantized anomalous Hall effect without chiral edge states, Phys. Rev. B 108, L241407 (2023).



