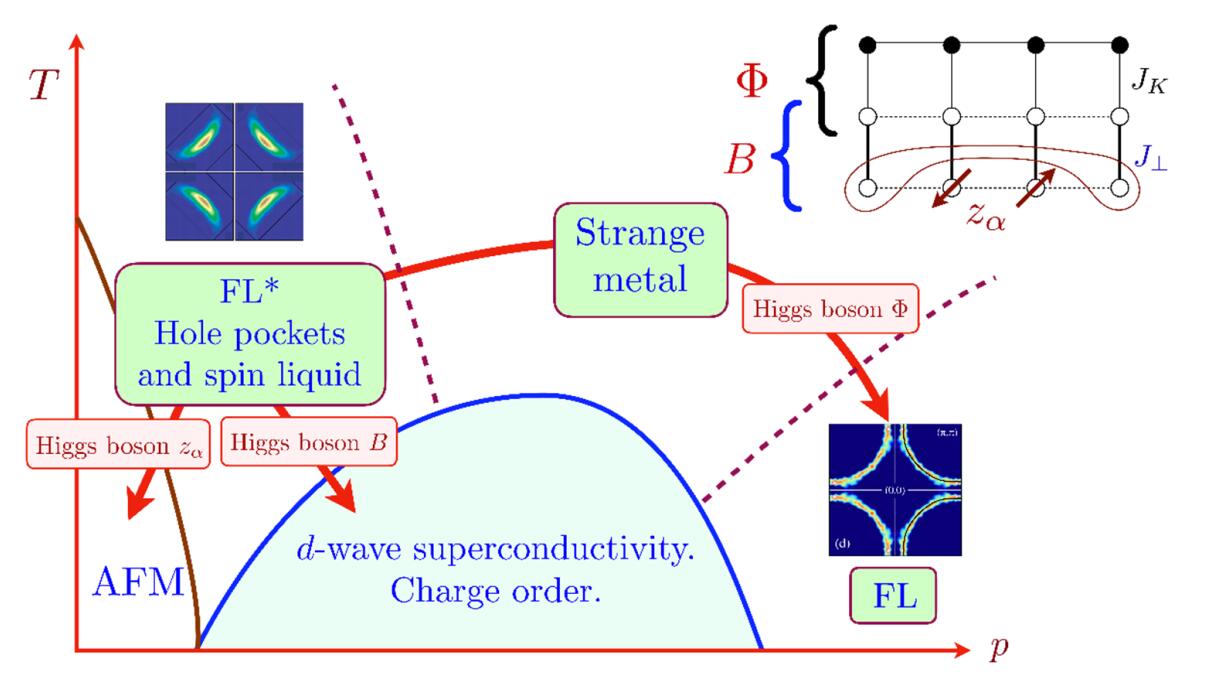
Soon after the discovery of high temperature superconductivity in the cuprates, Anderson proposed a connection to quantum spin liquids. But observations since then have shown that the low temperature phase diagram is dominated by conventional states, with a competition between superconductivity and charge-ordered states which break translational symmetry. We employ the "pseudogap metal" phase, found at intermediate temperatures and low hole doping, as the parent to the phases found at lower temperatures. We argue that the pseudogap is associated with a spin liquid, and that a particular spin liquid has the needed confining instabilities to resolve a number of open puzzles on the cuprate phase diagram.
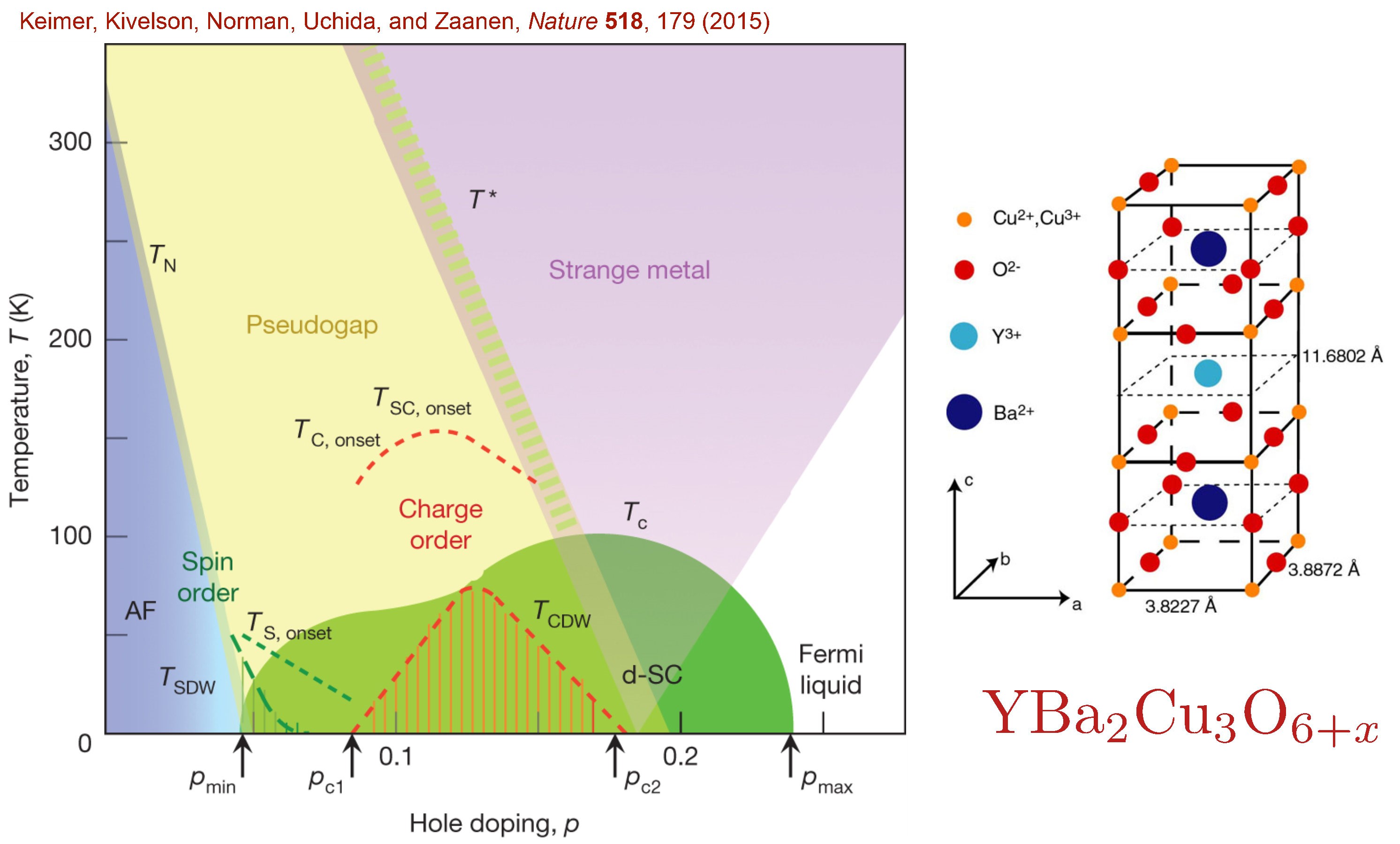
1. B. Keimer, S.A. Kivelson, M.R. Norman, S. Uchida, and J. Zaanen, From quantum matter to high-temperature superconductivity in copper oxides, Nature 518, 179 (2015).
2. Y. Qi and S. Sachdev, Effective theory of Fermi pockets in fluctuating antiferromagnets, Phys. Rev. B 81, 115129 (2010).
3. E. Mascot, A. Nikolaenko, M. Tikhanovskaya, Y.H. Zhang, D.K. Morr, and S. Sachdev, Electronic spectra with paramagnon fractionalization in the single-band Hubbard model, Phys. Rev. B 105, 075146 (2022).
4. K.Y. Yang, T.M. Rice, and F.C. Zhang, Phenomenological theory of the pseudogap state, Phys. Rev. B 73, 174501 (2006).
5. T.D. Stanescu and G. Kotliar, Fermi arcs and hidden zeros of the Green function in the pseudogap state, Phys. Rev. B 74, 125110 (2006).
6. C. Berthod, T. Giamarchi, S. Biermann, and A. Georges, Breakup of the Fermi surface near the Mott transition in low-dimensional systems, Phys. Rev. Lett. 97, 136401 (2006).
7. S. Sakai, Y. Motome, and M. Imada, Evolution of electronic structure of doped Mott insulators: reconstruction of poles and zeros of Green’s function, Phys. Rev. Lett. 102, 056404 (2009).
8. J. Skolimowski and M. Fabrizio, Luttinger's theorem in the presence of Luttinger surfaces, Phys. Rev. B 106, 045109 (2022).
9. J.C. Zhao, G. La Nave, and P. Phillips, Proof of a stable fixed point for strongly correlated electron matter, arXiv: 2304.04787 (2023).
10. Y.W Fang, G. Grissonnanche, A. Legros, S. Verret, F. Laliberté, C. Collignon, A. Ataei, M. Dion, J.S. Zhou, D. Graf, M.J. Lawler, P.A. Goddard, L. Taillefer, and B.J. Ramshaw, Fermi surface transformation at the pseudogap critical point of a cuprate superconductor, Nat. Phys. 18, 558 (2022).
11. T. Senthil, M. Vojta, and S. Sachdev, Weak magnetism and non-Fermi liquids near heavy-fermion critical points, Phys. Rev. B 69, 035111 (2004).
12. P.W. Anderson, Resonating valence bonds: a new kind of insulator?, Mater. Res. Bull. 8, 153 (1973).
13. G. Baskaran, Z. Zou, and P.W. Anderson, The resonating valence bond state and high-Tc superconductivity - a mean field theory, Solid State Commun. 63, 973 (1987).
14. S.A. Kivelson, D.S. Rokhsar, and J.P. Sethna, Topology of the resonating valence-bond state: solitons and high-Tc superconductivity, Phys. Rev. B 35, 8865 (R) (1987).
15. D.S. Rokhsar and S.A. Kivelson, Superconductivity and the quantum hard- core dimer gas, Phys. Rev. Lett. 61, 2376 (1988).
16. E. Fradkin and S. Kivelson, Short range resonating valence bond theories and superconductivity, Mod. Phys. Lett. B 4, 225 (1990).
17. S. Sachdev, Quantum phases of the Shraiman-Siggia model, Phys. Rev. B 49, 6770 (1994).
18. X.G. Wen and P.A. Lee, Theory of underdoped cuprates, Phys. Rev. Lett. 76, 503 (1996).
19. R.K. Kaul, A. Kolezhuk, M. Levin, S. Sachdev, and T. Senthil, Hole dynamics in an antiferromagnet across a deconfined quantum critical point, Phys. Rev. B 75, 235122 (2007).
20. E.G. Moon and S. Sachdev, Underdoped cuprates as fractionalized Fermi liquids: transition to superconductivity, Phys. Rev. B 83, 224508 (2011).
21. M. Punk, A. Allais, and S. Sachdev, Quantum dimer model for the pseudogap metal, Proc. Nat. Acad. Sci. 112, 9552 (2015).
22. A.A. Patel, H.Y. Guo, I. Esterlis, and S. Sachdev, Universal theory of strange metals from spatially random interactions, Science 381, 790 (2023).
23. E.E. Aldape, T. Cookmeyer, A.A. Patel, and E. Altman, Solvable theory of a strange metal at the breakdown of a heavy Fermi liquid, Phys. Rev. B 105, 235111 (2022).
24. W.O. Tromp, T. Benschop, J.F. Ge, I. Battisti, K.M. Bastiaans, D. Chatzopoulos, A.H.M. Vervloet, S. Smit, E. van Heumen, M.S. Golden, Y.K. Huang, T. Kondo, T. Takeuchi, Y. Yin, J.E. Hoffman, M.A. Sulangi, J. Zaanen, and M.P. Allan, Puddle formation and persistent gaps across the non-mean-field breakdown of superconductivity in overdoped (Pb,Bi)2Sr2CuO6+δ, Nat. Mater. 22, 703 (2023).
25. E. van Heumen, X.B. Feng, S. Cassanelli, L. Neubrand, L. de Jager, M. Berben, Y.K. Huang, T. Kondo, T. Takeuchi, and J. Zaanen, Strange metal electrodynamics across the phase diagram of Bi2−xPbxSr2−yLayCuO6+δ cuprates, Phys. Rev. B 106, 054515 (2022).
26. B. Michon, C. Berthod, C.W. Rischau, A. Ataei, L. Chen, S. Komiya, S. Ono, L. Taillefer, D. van der Marel, and A. Georges, Reconciling scaling of the optical conductivity of cuprate superconductors with Planckian resistivity and specific heat, Nat. Commun. 14, 3033 (2023).
27. T.J. Reber, X. Zhou, N.C. Plumb, S. Parham, J.A. Waugh, Y. Cao, Z. Sun, H. Li, Q. Wang, J.S. Wen, Z.J. Xu, G. Gu, Y. Yoshida, H. Eisaki, G.B. Arnold, and D.S. Dessau, A unified form of low-energy nodal electronic interactions in hole-doped cuprate superconductors, Nat. Commun. 10, 5737 (2019).
28. S.A. Hartnoll and A.P. MacKenzie, Colloquium: Planckian dissipation in metals, Rev. Mod. Phys. 94, 041002 (2022).
29. L. Wang and A.W. Sandvik, Critical level crossings and gapless spin liquid in the square-lattice spin-1/2 J1−J2 Heisenberg antiferromagnet, Phys. Rev. Lett. 121, 107202 (2018).
30. F. Ferrari and F. Becca, Gapless spin liquid and valence-bond solid in the J1-J2 Heisenberg model on the square lattice: insights from singlet and triplet excitations, Phys. Rev. B 102, 014417 (2020).
31. Y. Nomura and M. Imada, Dirac-type nodal spin liquid revealed by refined quantum many-body solver using neural-network wave function, correlation ratio, and level spectroscopy, Phys. Rev. X 11, 031034 (2021).
32. W.Y. Liu, S.S. Gong, Y.B. Li, D. Poilblanc, W.Q. Chen, and Z.C. Gu, Gapless quantum spin liquid and global phase diagram of the spin-1/2 J1-J2 square antiferromagnetic Heisenberg model, Sci. Bull. 67, 1034 (2022).
33. D.P. Arovas and A. Auerbach, Functional integral theories of low- dimensional quantum Heisenberg models, Phys. Rev. B 38, 316 (1988).
34. N. Read and S. Sachdev, Valence-bond and spin-Peierls ground states of low-dimensional quantum antiferromagnets, Phys. Rev. Lett. 62, 1694 (1989).
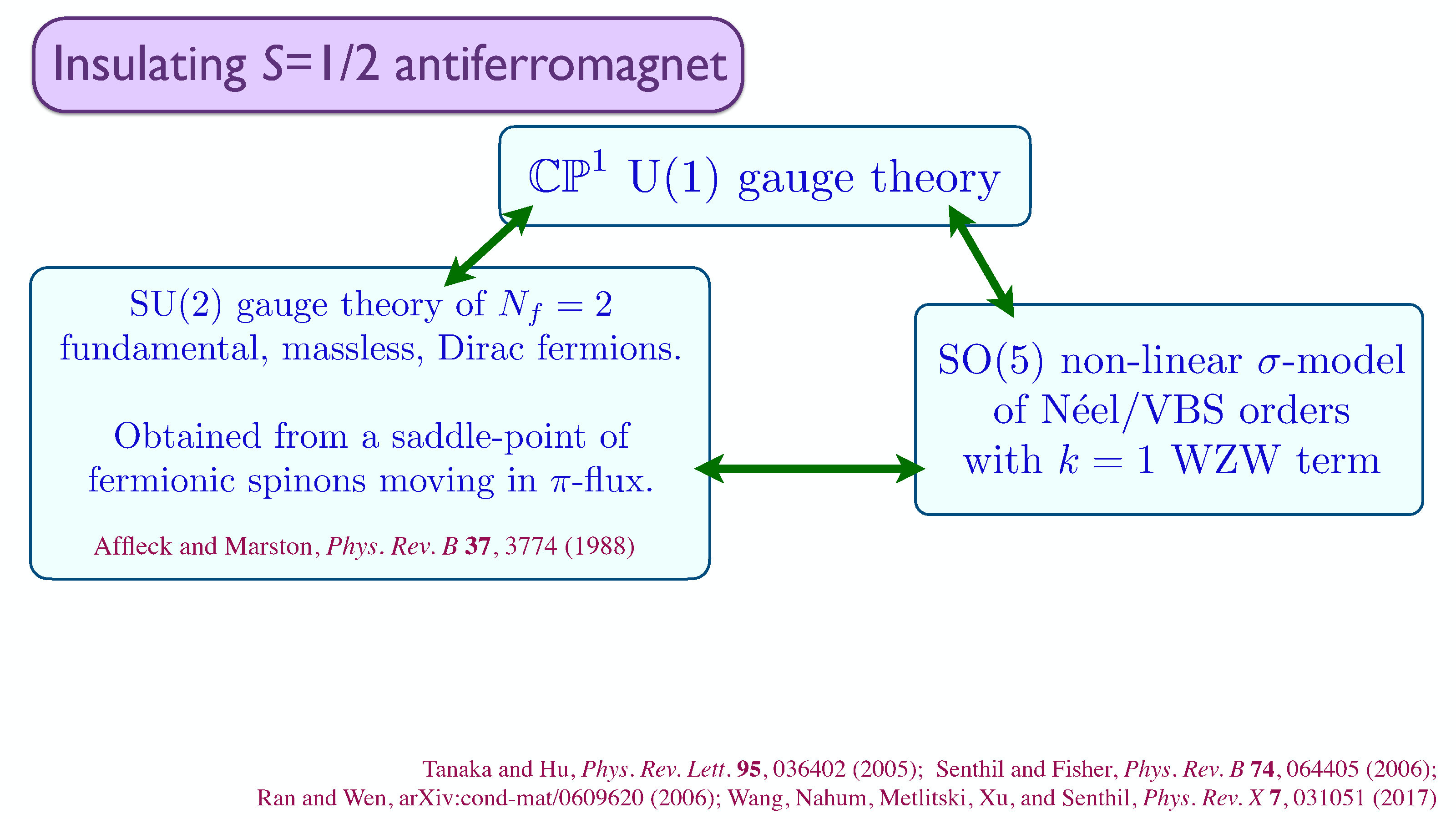
35. I. Affleck and J.B. Marston, Large-n limit of the Heisenberg-Hubbard model: implications for high-Tc superconductors, Phys. Rev. B 37, 3774(R) (1988).
36. A. Tanaka and X. Hu, Many-body spin berry phases emerging from the π- flux state: competition between antiferromagnetism and the valence-bond- solid state, Phys. Rev. Lett. 95, 036402 (2005).
37. T. Senthil and M.P.A. Fisher, Competing orders, nonlinear sigma models, and topological terms in quantum magnets, Phys. Rev. B 74, 064405 (2006).
38. Y. Ran and X.G. Wen, Continuous quantum phase transitions beyond Landau's paradigm in a large-N spin model, arXiv: cond-mat/0609620 (2006).
39. C. Wang, A. Nahum, M.A. Metlitski, C.K. Xu, and T. Senthil, Deconfined quantum critical points: symmetries and dualities, Phys. Rev. X 7, 031051 (2017).
40. A.W. Sandvik, Evidence for deconfined quantum criticality in a two- dimensional Heisenberg model with four-spin interactions, Phys. Rev. Lett. 98, 227202 (2007).
41. A. Nahum, P. Serna, J.T. Chalker, M. Ortuño, and A.M. Somoza, Emergent SO(5) symmetry at the Néel to valence-bond-solid transition, Phys. Rev. Lett. 115, 267203 (2015).
42. Z. Zhou, L.D. Hu, W. Zhu, and Y.C. He, The SO(5) deconfined phase transition under the fuzzy sphere microscope: approximate conformal symmetry, pseudo-criticality, and operator spectrum, arXiv: 2306.16435 (2023).
43. H.C. Jiang and S.A. Kivelson, High temperature superconductivity in a lightly doped quantum spin liquid, Phys. Rev. Lett. 127, 097002 (2021).
44. H.C. Jiang, S.A. Kivelson, and D.H. Lee, Superconducting valence bond fluid in lightly doped eight-leg t-J cylinders, Phys. Rev. B 108, 054505 (2023).
45. Y.H. Zhang and S. Sachdev, From the pseudogap metal to the Fermi liquid using ancilla qubits, Phys. Rev. Research 2, 023172 (2020).
46. R.H. He, M. Hashimoto, H. Karapetyan, J.D. Koralek, J.P. Hinton, J.P. Testaud, V. Nathan, Y. Yoshida, H. Yao, K. Tanaka, W. Meevasana, R.G. Moore, D.H. Lu, S.K. Mo, M. Ishikado, H. Eisaki, Z. Hussain, T.P. Devereaux, S.A. Kivelson, J. Orenstein, A. Kapitulnik, and Z.X. Shen, From a single-band metal to a high-temperature superconductor via two thermal phase transitions, Science 331, 1579 (2011).
47. M. Christos and S. Sachdev, Emergence of nodal Bogoliubov quasiparticles across the transition from the pseudogap metal to the d-wave superconductor, npj Quantum Mater. 9, 4 (2024).
48. N. Ma, G.Y. Sun, Y.Z. You, C.K. Xu, A. Vishwanath, A.W. Sandvik, and Z.Y. Meng, Dynamical signature of fractionalization at a deconfined quantum critical point, Phys. Rev. B 98, 174421 (2018).
49. M. Christos, Z.X. Luo, H. Shackleton, Y.H. Zhang, M.S. Scheurer, and S. Sachdev, A model of d-wave superconductivity, antiferromagnetism, and charge order on the square lattice, Proc. Nat. Acad. Sci. 120, e2302701120 (2023).
50. A. Nikolaenko, J. von Milczewski, D.G. Joshi, and S. Sachdev, Spin density wave, Fermi liquid, and fractionalized phases in a theory of antiferromagnetic metals using paramagnons and bosonic spinons, Phys. Rev. B 108, 045123 (2023).



